12.1 Rate of a Reaction

When we mix sulfuric acid H₂(SO)₄ with sugar, the mixture transforms into a large, black mound of carbon in a matter of minutes. If we expose steel, which contains iron, to humidity and atmospheric oxygen, visible rust, Fe₂O₃, takes at least several days to form.  

C₁₂H₂₂O₁₁(s) + 11H₂₍SO₄)(l) → 12C(s) +  11H₂₍SO₄) • H2O(l) 

and  

4Fe + 3O₂ → 2Fe₂O₃ 

Both reactions are spontaneous reactions and exothermic at ambiEnt temperature, yet one takes far longer than the other. Why? Chemical kinetics may offer an explanation.   

White Rust by darkday 

Chemical kinetics is about chemical process’ rates and the mechanisms that speed up or slow down reactions. Studying these mechanisms often means taking a close look at molecular level interactions, intermediate steps, and energy needed to start even exothermic reactions.  

Thermodynammics Points the Way 

Let’s start with an equation:  

Energetics + dynamics = chemical change 

During reactions molecules rearrange in a way that increases their disorder  and reduces potential energy by giving off heat. This means that a chemical system tries to reduce its free energy ∆G to the lowest point possible. When a chemical system reaches the minimum free energy possible, the forward and backward reaction reach equal rates. The forward reaction appears to stop, and the system is at equillibrium.  

If we know reactants and products ∆Gs, we can predict whether a forward or backward reaction is exothermic (spontaneous), and the equillibrium state’s composition. We will not, however, know the forward or backward reaction’s speed.  

Rate of reaction is independent of changes in free energy, ΔG°, or enthalpy, ΔH°. We only discover reaction rates experimentally, because while we can measure molar proportions with stoichiometry, these measurements give no clue to the twisting, stretching, breaking and reforming of molecular bonds that goes on behind the scenes. 

Let’s look at reactions that create hydrogen halides. The three reactions share stoichometry, but NOT mechanisms. 

H2(g) + I2(g) → 2 HI(g)	H2(g) + Br2(g) → 2 HBr(g)	H2(g) + Cl2(g) → 2 HCl(g)
Hydrogen and iodine join via the simplest imaginable mechanism: a collision between the two reactant molecules rearranges their bonds	The reaction between hydrogen and bromine reaction follows a succession of steps, some of which involve atomic H and Br.	A mixture of hydrogen and chlorine will not react at all in the dark, but with light, it goes off with a bang as the instantaneous reaction releases heat and expands the gases explosively.

Rates of Chemical Reactions 

Think of the examples that began this chapter. Reaction speeds range from nearly instantaneous to years, but chemists define reaction speed as chang in concentration of a substance divided by time. [Brackets] are our symbol for concentration, and ∆ time is t2 – t1 (new time minus old).  

For A + B → C, we can write its rate using change in any of its components’ concentration. 

Fig. 12.1 

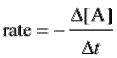Notice that ∆[A] and ∆[B] both have negative signs. That is because they are reactants which the reaction uses up. That means they decrease with time and would give a negative rate or reaction unless multipied by minus one.  

When a chemical reaction includes coefficients that are different, we divide each reactant’s change by its coefficient.  

In the reaction: A + 3B → 2D, rate equations are: 

rate  = –∆A/∆t 

rate = –∆B/3∆t 

rate =  ∆D/2∆t 

And yes, we can determine reaction rate if we know the change in concentration of any ONE of its components or products and the time elapsed. All three equations above equal the same thing!   

Problem Example 1 

For the oxidation of ammonia 4 NH3 + 3O2 = 2 N2 + 6 H2O 

it was found that the rate of formation of N2 was 0.27 mol L–1 s–1. 

a) What is the rate of formation for water? 

b)  What is the rate of consumption for amonia? 

Solution: 

a) From the equation stoichiometry, Δ[H2O] = 6/2 Δ[N2], so the rate of formation of H2O is 3 × (0.27 mol L–1 s–1) = 0.81 mol L–1 s–1. 

b) 4 moles of NH3 are consumed for every 2 moles of N2 formed, so the rate of disappearance of ammonia is 2 × (0.27 mol L–1 s–1) = 0.54 mol L–1 s–1. 

Comment: We could  also express amonia’s disappearance rate as a negative number. 

Here is a YouTube 

Instantaneous rates 

As, the curving line in Figure 12.3 shows, rate of reaction is NOT linear. Most reactions slow as they approach equillibrium, and a single constant for rate for the entire time of reaction, is not particularly precise.  

Fortunately, we can measure the rate of reaction at various times. Figure 12.3 represents these instantaneous rates as slopes of tangents to the main reaction rate line. Of particular interst is rate #1, the rate at the beginning of the reaction or initial rate. Initial rates are especially helpful in determining chemical kinetics. (See below.) 

Instantaneous rates are also derivatives of the reaction rate curve at given points in time. These slopes approach a limit of zero, becoming nearly horizontal at equillibrium.  

It would be really great to have a picture with the curve that had a single regression line (single rate like what we took above) going through it to show how imprecise this measurement is.  

Determination of Reaction Rates 

Fig. 12.5  This is a chemical reaction.  

Table 12.2 This shows concentration and average rate at fifty second intervals for butane chloride C₄H₉Cl in the above equation.  

If we plot the concetration of C₄H₉Cl from Table 14.1 against time, we get a concave curve with a negative slope. The slope is negative because this reaction consumes C₄H₉Cl.   If we take the curve’s slope at different time points, we obtain instananeous rates. The rate taken at t₀ or the start of the reaction is the initial rate.  

Relative Rates 

In the case of the C₄H₉Cl  → C₄H₉OH, butyl chloride uses up as quickly as butyl hydroxide’s is created, but would that be the case where reactants and/or products have different coefficients?  

Relative Rates and Stoichometry 

Rate for each reactant or product depends on stoichiometry If we followed use of C4H9Cl and compared it to production of C4H9OH, the values would be the same. Note that the change would have opposite signs—one goes down in value, the other goes up. 

Let’s look at an example with a reactant-product ration that is not 1:1. What are ozone to oxygen’s relative rates be for: 

2 O3 (g)  →  3 O2 (g) 

Here is another example: 

N₂O₄⇌2NO₂ 

Multiplying ∆t in the demonimator by the stoichoiometric coefficient enables average rate calculation.  

-∆[ N₂O₄]/ ∆t = ∆[ NO₂]/2∆t 

A more generalized formula is  

-(1 ∆ [A])/(ν dt)=(1 ∆ [B])/(ν dt)=r(t)=k[A]^order  

∆[A] = change in concentration of a reactant or product.  

∆[B] = change in concentration of a reactant or product.  

v = stoichometric coefficients  

k = rate constant (Make sure to write this in lower case, so as not to confuse it with K_eq) 

order = Is the sum of the influence of reactants concentration on reaction rate.  

r = is a mystery variable. 

We will cover order later, but because N₂O₄ is the only reactant order is one (1).  

-∆ [N2O4]/ ∆ t=∆ [NO2]/2*( ∆t)=r(t)=k[N2O4]¹  

Once we tuck them into the denominator of an average rate equations, stoichiometric coefficients do not effect therate law, thoughthey do effect the rate constant, k. (Remember to write this in lower case.) 

Therefore, the stoichiometric coefficients do not affect how the rate law is written, but they do affect the value of the rate constant k.